| 元素名 | 同位体及びその存在比(%) | ||
|---|---|---|---|
| 炭 素 | 12C 100 | 13C 1.08 | |
| 水 素 | 1H 100 | 2H 0.016 | |
| 酸 素 | 16O 100 | 17O 0.04 | 18O 0.20 |
| 塩 素 | 35Cl 100 | 37Cl 32.6 | |
| 臭 素 | 79Br 100 | 81Br 98.0 | |
有機化合物を構成する主要元素は炭素、水素、酸素であるが、それぞれ質量数の異なる安定同位体が存在する。右表は主な各原子の同位体の天然存在比を示したものである。同位元素の天然存在比はハロゲンを除けばいずれも少なく無視できるかに見える。しかし、質量分析計は検出感度の高い測定が可能な分析機器である。したがって、元素組成が同じであっても質量数の異なるピーク(同位体ピークという)を検出することができる。1-phenyl-1-butanoneの質量スペクトルを見てわかる(→こちらを参照)ように、分子イオンピーク(M+)のほか、イオン強度は小さいながら(M++1)のピークm/z 149が見られる。これが同位体ピークである。そのほか、イオン強度の大きいピークの脇にも(+1)ピークが見られるが、これにも同位体ピークによる寄与が一部含まれている。各元素の安定同位体の存在比は一定であるので、同位体ピークの相対強度も一定となるはずである。ここでCxHyOzという組成の分子の同位体ピークの相対強度を計算してみよう。まず、「存在比とは存在確率と同義である」ことを理解すれば、同位体ピークの相対強度を求めることはそれぞれの「存在確率を計算する」ことに等しいことがわかる。話を簡潔かつ円滑にに進行させるため、12C、13C、1H、2H、16O、17O、18Oをそれぞれの同位体の存在比(存在確率)をも表わすとする。簡単な数学の確率論により、CxHyOzという分子の全ての同位体ピークを羅列しそれぞれのピーク強度を計算するには、下の式に示すように、(12C+13C)x(1H+2H)y(16O+17O+18O)zを展開すればよいことになる。この式を展開して得られる各項は各同位体の組み合わせに相当し、それぞれの存在比を代入して計算すれば相対強度と同義のものとなる。但し、存在比の小さな同位体同士の組み合わせは無視できるので、下の式のような近似式で表わすことができる。
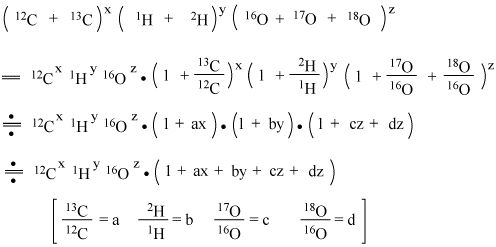
いわゆる分子イオンピーク(M+)の存在確率は上の式では(12C)x(1H)y(16O)zであり、(M++1)は[(12C)x(1H)y(16O)z](ax+by+cz)、(M++2)は[(12C)x(1H)y(16O)z)](dz)で表わされるので、分子イオンピークに対する相対強度比は1 : (ax+by+cz) : (dz)となる。実際、C10H12Oの分子式で表わされる1-phenyl-1-butanoneの場合では、1 : 0.110 : 0.002となる。この場合、(M++2)ピークは無視できるが、(M++1)ピークすなわちm/z 149は分子イオンピークの約9分の1の強度で出現することになり、決して無視できるレベルではないことがわかる。また、この一般式から分子量が大きくなればなるほど分子イオンピークに対する同位体ピークの相対強度が大きくなることがわかる。
以上は炭素、水素、酸素から構成される有機化合物の同位体ピークについて言及したが、中には存在比の高い同位元素をもつ原子もあり、それを含む化合物では同位体ピークの存在はとりわけ顕著となる。例えば、塩素では35Clと37Clが100:32.6の割合で天然に存在するので、塩素原子1個もつ分子の質量スペクトルでは分子イオンピークとしてM+(35Clによるピーク)とM++2(37Clによるピーク)が100:32.6の割合で出現する。そのほか、臭素では79Brと81Brが100:98.0の割合で存在するので、分子イオンピークは(M+):(M++2)=100:98.0となる。
ここで分子内に臭素原子2個と塩素原子1個もつ分子について考えてみよう。この場合、分子イオンピークはM+、M++2、M++4、M++6の4本となるのでそのピーク強度比を計算する。計算を簡略化するため存在比を次のようにする。
- 35Cl : 37Cl=3 : 1
- 79Br : 81Br=1 : 1
前述したように同位体ピークは同位体の組み合わせの結果であり、一方、ピーク強度比はそれぞれの組み合わせの存在比(存在確率)を反映したものである。ここでは、よりわかりやすくするため、可能な同位体の組み合わせの全てをリストアップしてみよう。その場合、臭素は2個あるのでそれぞれに番号をつけてBr(1)、Br(2)として区別する必要がある。その結果は下の表のようになるはずである。各組み合わせの存在確率は各同位体の存在比の積(掛け合わせたもの)に相当(この場合、比だけを求めればよいので35Cl の存在確率を3、その他を1とした←前述の天然存在比の数字をそのまま流用した)し、各ピークの強度比は可能な組み合わせの和になる。その結果を次に示すが、これによると予想される強度比は3:7:5:1となる。実際の存在比を基にした計算結果は100:228.0:159.0:31.2であり、簡略化してもかなり近似の値を得ることができることがわかる。
| 同位体ピーク | 同位体組み合わせ | 存在確率 | 存在比 |
|---|---|---|---|
| M+ | 79Br(1)79Br(2)35Cl | 1x1x3 | 3 |
| M++2 | 81Br(1)79Br(2)35Cl | 1x1x3 | |
| 79Br(1)81Br(2)35Cl | 1x1x3 | 7 | |
| 79Br(1)79Br(2)37Cl | 1x1x1 | ||
| M++4 | 81Br(1)81Br(2)35Cl | 1x1x3 | |
| 79Br(1)81Br(2)37Cl | 1x1x1 | 5 | |
| 81Br(1)79Br(2)37Cl | 1x1x1 | ||
| M++6 | 81Br(1)81Br(2)37Cl | 1x1x1 | 1 |
この場合はBr2Cl1という簡単な組み合わせなので、全ての組み合わせをリストアップするのは容易であるが、BrxClyのような任意の式で表わされる場合は前述の方法を用いて計算する。すなわち、(79Br+81Br)x(35Cl+37Cl)yを数式として展開し、各項を計算すればよい。但し、この場合は同位体の存在比が大きいので近似計算はできない。実際に、x=2、y=1として計算してみると下のようになる。この結果は組み合わせをリストアップして得た上の結果と一致していることが理解されよう。つまり、前述の式を機械的に展開すればどんな組み合わせでも求めることができることになる。
